Next: 7 Goldener Schnitt Up: Über Fibonacci-Folgen Previous: 5 Teilbarkeiten Index
Wie in 1.1 bereits erwähnt, bilden Fibonacci-Folgen gewissermaßen einen Gegenpol zu den Zweierpotenzen.
Die Zweierpotenzen lassen sich durch b0 : = 1; bn : = bn-1 + bn-1 = 2bn-1 definieren und bilden als geschlossene Form den Term bn = 2n. Ist es auf ähnliche Weise möglich, die Fibonacci-Folge in eine geschlossene Form zu pressen? - Nun ja, manche Erkenntnis fällt vom Himmel, und manchmal muß man dazu etwas nachhelfen. Schießen wir also etwas Silberjodid in die Wolken und warten ab, was herunterkommt...
Der Ansatz lautet,
fn = xn zu setzen, und wir erhalten damit
aus der Rekursionsgleichung
fn = fn-1 + fn-2 die Gleichung
xn = xn-1 + xn-2, die (für x ![]() 0) zu x2 = x + 1 äquivalent
ist. Diese wiederum entspricht
x2 - x - 1 = 0, dem sogenannten »charakteristischen
Polynom« der zugehörigen Rekursion. Wir ermitteln nun dessen Nullstellen,
in dem wir eine quadratische Ergänzung auf beiden Seiten addieren:
0) zu x2 = x + 1 äquivalent
ist. Diese wiederum entspricht
x2 - x - 1 = 0, dem sogenannten »charakteristischen
Polynom« der zugehörigen Rekursion. Wir ermitteln nun dessen Nullstellen,
in dem wir eine quadratische Ergänzung auf beiden Seiten addieren:
(Die quadratische Ergänzung wird bestimmt durch den Ansatz
(x + y)2 = x2 +2xy + y2,
wobei hier 2xy = - x gewünscht wird. Also
y = - ![]() .)
.)
![]()
![]()
![]()
![]()
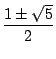
Wie man es bei quadratischen Gleichungen nicht anders erwarten kann, erhalten wir zwei Lösungen. Nun ja, wir haben ja auch zwei Startwerte f0 und f1, die wir bisher noch nicht ins Spiel gebracht haben. Versuchen wir eine Linearkombination der beiden Lösungen, um eine von den Startwerten abhängige geschlossene Form zu erhalten6:
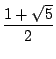 )n + b . (
)n + b . (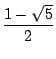 )n
)n
Für f0, also n = 0 erhalten wir daraus
f0 = a . (![]() )0 + b . (
)0 + b . (![]() )0 = a + b.
Für f1 ergibt sich
f1 = a . (
)0 = a + b.
Für f1 ergibt sich
f1 = a . (![]() ) + b . (
) + b . (![]() ).
Das ist ein lineares Gleichungssystem mit zwei Gleichungen und zwei
Unbekannten und sollte sich daher lösen lassen:
).
Das ist ein lineares Gleichungssystem mit zwei Gleichungen und zwei
Unbekannten und sollte sich daher lösen lassen:
Mit b = f0 - a (aus der ersten Gleichung) ergibt sich eingesetzt in die zweite
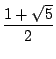 + (f0 - a)
+ (f0 - a)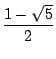
![]()
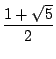 + f0
+ f0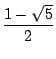 - a
- a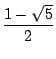
![]()
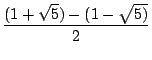 + f0
+ f0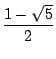
![]()
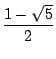
![]()
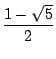
![]()
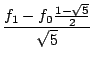
Für die Fibonacci-Folge Fn mit F0 = 0 und F1 = 1 ergibt
dies
a = ![]() und
b = 0 - a = -
und
b = 0 - a = - ![]() , also
Fn =
, also
Fn = ![]() (
(![]() )n -
)n - ![]() (
(![]() )n =
)n = ![]() -
- ![]() =
= ![]() .
.
Unter Berücksichtigung der Tatsache, daß
(1 + ![]() ) - (1 -
) - (1 - ![]() ) = 2 .
) = 2 . ![]() ist, ergibt sich
Fn =
ist, ergibt sich
Fn = ![]() . (
. (![]() )n-1 =
)n-1 = 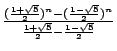 die sogenannte »binetsche Darstellung« der Fibonacci-Folge, die,
wenn wir
die sogenannte »binetsche Darstellung« der Fibonacci-Folge, die,
wenn wir
![]() : =
: = ![]() und
und
![]() : =
: = ![]() setzen, in der Form
Fn =
setzen, in der Form
Fn = ![]() besonders einprägsam ist.
besonders einprägsam ist.
Unter Anwendung von 4.1.2 erhalten wir beinahe unmittelbar auch deren allgemeine geschlossene Darstellung geschenkt:
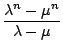 + f0
+ f0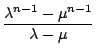 =
= 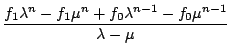
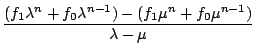 =
= 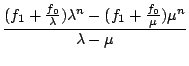
Thorsten Reinecke 2004-07-11