8 Noch eine Berechnungsmethode für Fibonaccizahlen

Auf die folgende Berechnungsmethode bin ich gestoßen, als ich die Eigenschaften von $\lambda$ näher untersucht habe. Dabei dürfte ich wohl ein mir bisher unbekanntes Verfahren »wiederentdeckt« haben.⁷ Vielleicht ist die Herleitung aber interessant:

Betrachten wir das charakteristische Polynom x² - x - 1. Nullsetzen ergibt x² = x + 1. Die Nullstellen sind $\lambda$ und $\mu$. Für diese gilt x² = x + 1.

Für x³ erhalten wir daraus x³ = x^{2 .} x = (x + 1) ^. x = x² + x = (x + 1) + x = 2x + 1 = F₃ ^. x + F₂; analog ergibt sich induktiv

xⁿ = x^{n-1 .} x = (F_n-1 ^. x + F_n-2) ^. x = F_n-1 ^. x² + F_n-2 ^. x = F_n-1 ^. (x + 1) + F_n-2 ^. x

= F_n-1 ^. x + F_n-1 + F_n-2 ^. x = (F_n-1 + F_n-2) ^. x + F_n-1 = F_n ^. x + F_n-1

Mit diesem Wissen können wir die geschlossene Form auch einfach ausrechnen:

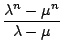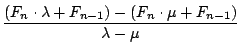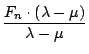$${\frac{{\lambda^{n}-\mu^{n}}}{{\lambda-\mu}}}$$ = $${\frac{{(F_{n}\cdot\lambda+F_{n-1})-(F_{n}\cdot\mu+F_{n-1})}}{{\lambda-\mu}}}$$ = $${\frac{{F_{n}\cdot(\lambda-\mu)}}{{\lambda-\mu}}}$$ = F_n

ebenso:

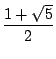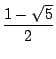$$\lambda^{{n}}_{}$$ + $$\mu^{{n}}_{}$$ = (F_n$$\lambda$$ + F_n-1) + (F_n$$\mu$$ + F_n-1) = F_n ^. ($$\lambda$$ + $$\mu$$) + 2F_n-1 = F_n ^. ($${\frac{{1+\sqrt{5}}}{{2}}}$$ + $${\frac{{1-\sqrt{5}}}{{2}}}$$) + 2F_n-1

= F_n +2F_n-1 = F_n + F_n-1 + F_n-1 = F_n+1 + F_n-1 = L_n

8.0.0.1 Eine neue Struktur

Kennen Sie komplexe Zahlen? Ähnlich, wie man diese konstruiert, können wir auch hier vorgehen: Definiere a : = (a₁, a₂) : = a₁ ^. $\lambda$ + a₂; analog sei b : = (b₁, b₂) : = b₁ ^. $\lambda$ + b₂.

Die Definition eines solchen Zahlenpaares ist in dem Sinne eindeutig, dass es eine reelle Zahl darstellt, welche nicht durch ein anderes Paar aus rationalen (und daher erst recht nicht natürlichen) Zahlen gebildet werden kann. Denn sei z.B. a = b, also a₁ ^. $\lambda$ + a₂ = b₁ ^. $\lambda$ + b₂, dann folgt (a₁ - b₁) ^. $\lambda$ = b₂ - a₂, womit die rechte Seite der Gleichung entweder null oder ebenfalls irrational sein muß.

Mit obiger Definition gelten folgende Rechenregeln:

a + b = (a₁, a₂) + (b₁, b₂) = (a₁$$\lambda$$ + a₂) + (b₁$$\lambda$$ + b₂) = (a₁ + b₁)$$\lambda$$ + (a₂ + b₂) = (a₁ + b₁, a₂ + b₂)

a ^. b = (a₁, a₂) ^. (b₁, b₂) = (a₁$$\lambda$$ + a₂)(b₁$$\lambda$$ + b₂) = a₁$$\lambda$$b₁$$\lambda$$ + a₁$$\lambda$$b₂ + a₂b₁$$\lambda$$ + a₂b₂

= a₁b₁$$\lambda^{{2}}_{}$$ + (a₁b₂ + a₂b₁)$$\lambda$$ + a₂b₂ = a₁b₁($$\lambda$$ +1) + (a₁b₂ + a₂b₁)$$\lambda$$ + a₂b₂

= a₁b₁$$\lambda$$ + a₁b₁ + (a₁b₂ + a₂b₁)$$\lambda$$ + a₂b₂ = (a₁b₁ + a₁b₂ + a₂b₁)$$\lambda$$ + a₁b₁ + a₂b₂

= (a₁b₁ + a₁b₂ + a₂b₁, a₁b₁ + a₂b₂)

In dieser Struktur kann man also »addieren« und »multiplizieren«. Wir stellen fest, daß $\lambda^{{0}}_{}$ = 1 = (0, 1), $\lambda^{{1}}_{}$ = $\lambda$ = (1, 0), $\lambda^{{2}}_{}$ = $\lambda$ + 1 = (1, 1) und allgemein gilt: $\lambda^{{n}}_{}$ = F_n ^. $\lambda$ + F_n-1 = (F_n, F_n-1). Dies liefert uns ein Verfahren, um (F_n, F_n-1) durch schnelle Exponentiation (durch fortgesetztes Quadrieren mit anschließendem Zusammenmultiplizieren der zu den Zweierpotenzen gehörigen Quadrate) zu bestimmen. Die Lösung für allgemeine Fibonaccifolgen ergibt sich dann mittels 4.1.2.

8.0.0.2 Algorithmus

Der Algorithmus cap:ExpoAlgorithmus erwartet ein Fibonaccizahlenpaar x : = (f₁, f₀) mit den Startwerten der Fibonaccifolge sowie den Index n und liefert dann das Paar (f_n, f_n-1) als Ergebnis zurück.

8.0.0.2.1 Bemerkungen:

1. Der Ausdruck (n and i) steht für den komponentenweisen and-Operator: Genau diejenigen Bits, die sowohl in n als auch in i gesetzt sind, sind auch im Ergebnis gesetzt. Der Ausdruck ist genau dann als wahr zu interpretieren, wenn mindestens ein Bit im Ergebnis gesetzt ist.
2. Für r ^. q kommt man mit drei skalaren Multiplikationen aus, wenn man h1 : = (r1 + r2)(q1 + q2) = r1 ^. q1 + r1 ^. q2 + r2 ^. q1 + r2 ^. q2; h2 : = r1 ^. q1; h3 : = r2 ^. q2 setzt. Es ergibt sich (r1 ^. q1 + r1 ^. q2 + r2 ^. q1, r1 ^. q1 + r2 ^. q2) = (h1 - h3, h2 + h3).
3. Die Anzahl der erforderlichen Multiplikationen für q ^. q kann man auf zwei reduzieren, in dem man die Lucasfolge verwendet: h1 : = q1 + 2 ^. q2 = F_i +2F_i-1 = L_i; h2 : = h1 ^. h1 - (- 1)^{i .} 2 = L_i² - (- 1)^{i .} 2 = L_2i; h3 : = q1 ^. h1. Es ergibt sich (q1 ^. q1 + 2 ^. q1 ^. q2, q1 ^. q1 + q2 ^. q2) = (F_2i, F_2i-1) = (F_i ^. L_i,${\frac{{L_{2i}-F_{2i}}}{{2}}}$) = (h3,${\frac{{h2-h3}}{{2}}}$).
4. Wird die Funktion häufig und mit vielen verschiedenen Werten aufgerufen⁸, so kann man die Quadrate vorab berechnen und in einem Array speichern.

8.0.0.2.2 Ausblick:

Es geht noch schneller, wenn man die binäre Exponentiation ein wenig umgestaltet und vom höchstwertigen Bit abwärts verlaufen läßt; abhängig vom jeweiligen Bit ist dann entweder (F_2i, F_2i-1) oder (F_2i+1, F_2i) zu bestimmen. Dabei kommt man mit reinen Quadrierungsschritten aus und kann die Multiplikationen einsparen. Für jeden Schritt sind dann nur noch zwei skalare Quadrierungen sowie einige billige Operationen (Addition, Subtraktion, Shiften) erforderlich. Erläuterungen hierzu und eine Implementierung finden sich beispielsweise in [GNU MP]. - Solche »Exponentiationsalgorithmen« kann man auch allgemein betrachten und weiteren Optimierungen unterziehen (wobei sich wiederum ein Bezug zu den Fibonaccizahlen ergibt); siehe [PLMo92] für eine solche Untersuchung.